こんにちは、株式会社COMPASS 教育R&Dの木川です。
前編に続き、青島小学校の取り組みについて、個別最適な学びの実践例をお届けします。
個別最適な学びの実践例
①第1~7時 「教科書の単元計画を基に計画を立て、振り返る」
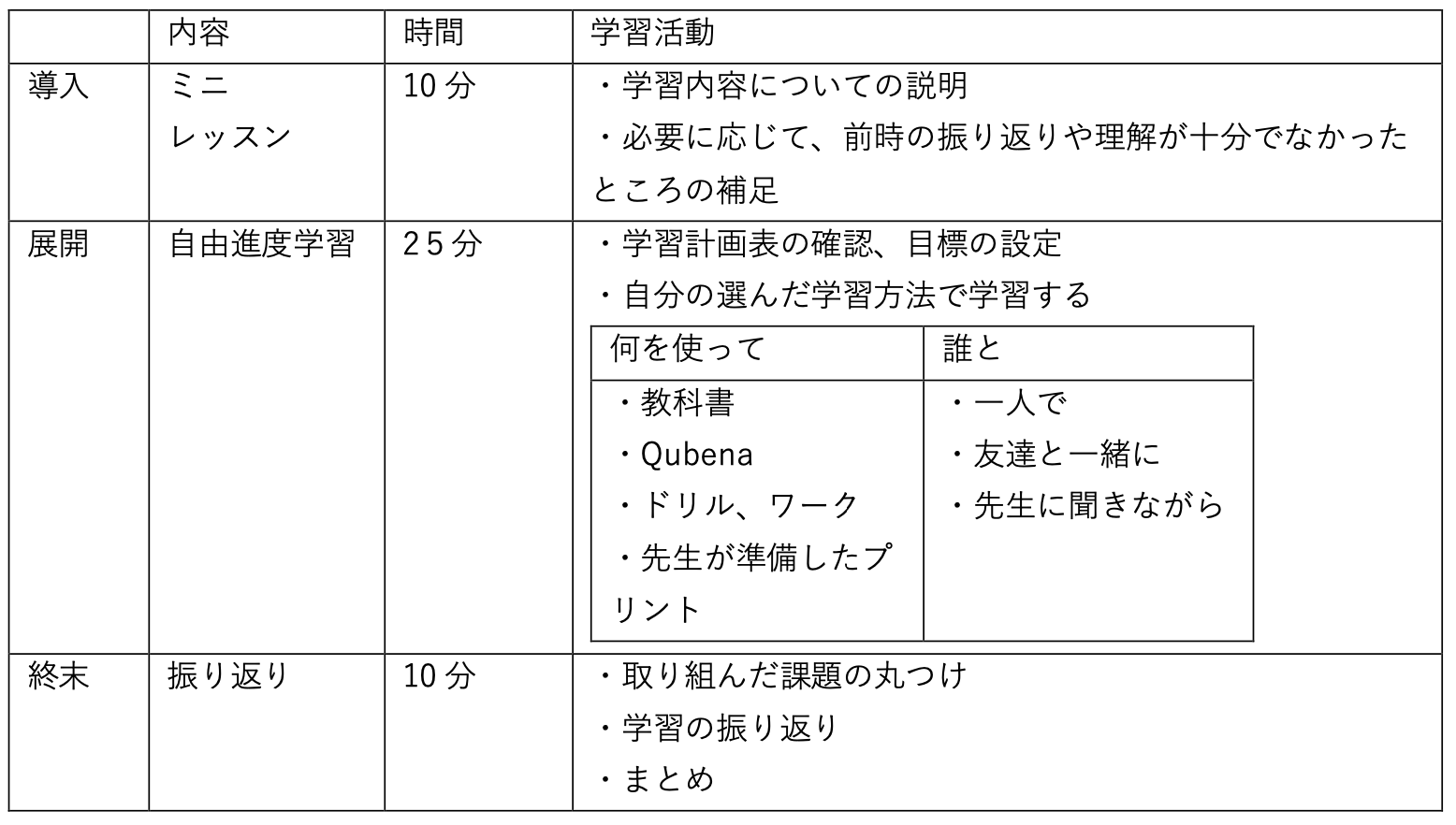
導入 ミニレッスン
導入のミニレッスンでは、教科書の単元計画に従って、本時の学習内容の大まかな説明を行います。
従来は、1コマ45分の時間をかけて、学習課題の提示→個人思考→集団思考→まとめと順を追って理解させていく内容を、重点を絞って10分程度で伝えます。あらかじめ資料にまとめた本時の内容を、子供たちと対話しながらテレビや黒板に提示して説明するイメージです。
このミニレッスンの目的は、学習内容の「理解」ではなく、学ぶ対象の「認識」と捉えていただくと良いと思います。何を学ぶのかの認識合わせが児童と出来れば、その後は児童主体で学習が進んでいきます。なお、児童によってはこのミニレッスンの内容より先に進んでいることもありますが(自由進度なので)、その場合でもこの時間は学ぶ対象の再認識の時間として有用であるため、他の児童と同様に聞いてもらいます。
展開 自由進度学習
次に展開の部分の自由進度学習では、最初に何を使ってどのように学ぶのかという学習方法と、自分の目標を決めていきます。
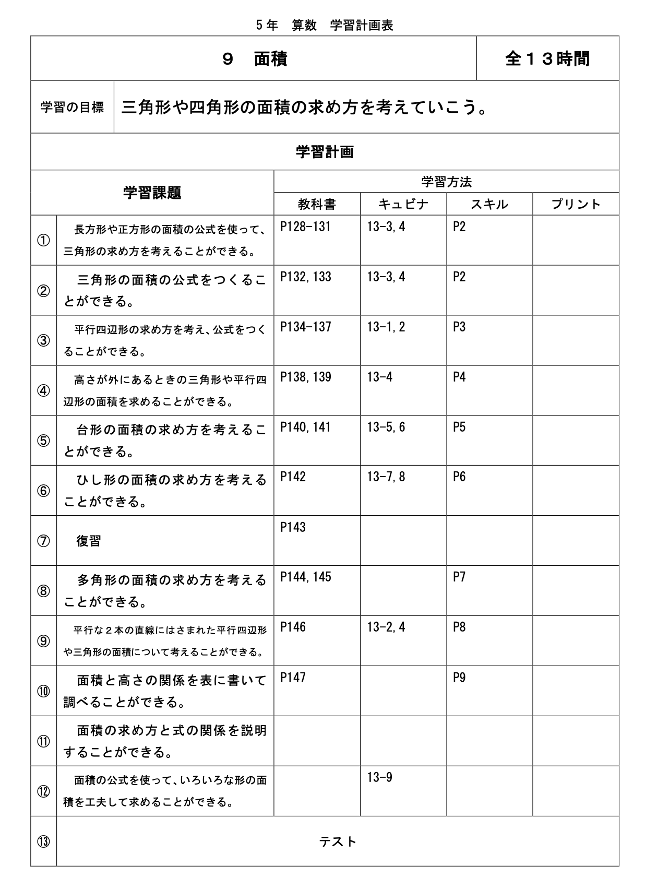
単元の始めに下図のような学習計画表を配り各自計画を立てるので、これをもとにその日の達成目標を決めます。そのため、これまでのような全員一緒のめあて(目標)にはなりません。
また、理解がゆっくりな児童は、その日のミニレッスンで扱った学習内容よりも手前の範囲を目標とすることもありますが、それが本人にとって必要なのであれば、むしろ好ましい判断であるため尊重します。一方で、教師側はそうした状態であることを認識し、念入りに学習状況を見取り、必要に応じてサポートします。
自由進度学習を行っている時の様子ですが、教科書、Qubena、市販の問題集、教師が準備したプリントなど、自由に自分に合うものを選んで学習しています。大部分の児童が自分にあった問題が出題されるQubenaを選びますが、他の教材と組み合わせて学習することが多いです。
また、一人ひとりが黙々と学んでいるわけではなく、友達と一緒にグループを作ってやっている児童、席を離れて、友達に聞きに行く児童、先生を呼ぶ児童など、授業自体は賑やかな雰囲気で進んでいきます。児童には「困ったら質問しよう」「困っている人がいたら教えてあげよう」ということを伝えているので、自然と学び合いも始まっていきます。(もちろん一人で黙々とやりたい児童もいますので、それも尊重しながらですが。)
本校では、3年生以上の算数の指導をティーム・ティーチングで行っています。自由進度学習では、T1が主に全体的な進捗状況を確認しながら、学習方法で困っていたり、分からないところがあったりする児童へサポートします。T2は、特に理解に時間がかかる児童を中心にサポートします。


終末 振り返り
終末の10分間は振り返りの時間で、一番大事にしたい時間です。
児童は自分が取り組んだ課題の丸付けをした後、自分の学習を振り返ります。目標が達成できたかどうかということも重要ですが、それ以上に今日は自分がどんなことを学んだかや、どこを特に間違えていたのかという間違いの分析をするように伝えています。
例えば、単純な計算間違いでも「筆算のこの部分の足し算で間違えた」など、具体的に分析して書くことを伝えます。振り返りが書けたら、それをロイロノートで全員提出してもらい、全体に公開して、友達の分析や記述の良さを共有しています。

②第8~10時 「これまでに得た知識や技能を使って更に思考を深めていく」
この時間は、これまでに得た知識や技能を使って更に思考を深めていく内容のため、ミニレッスンと自由進度学習ではなく通常のスタイルで授業を進めていきます。板書やスライドなどイメージしやすい資料を用いて説明をしていきます。
③第11~12時 「最後に応用的な問題に取り組む」
単元の最後に2時間を使って応用的な問題に取り組みます。
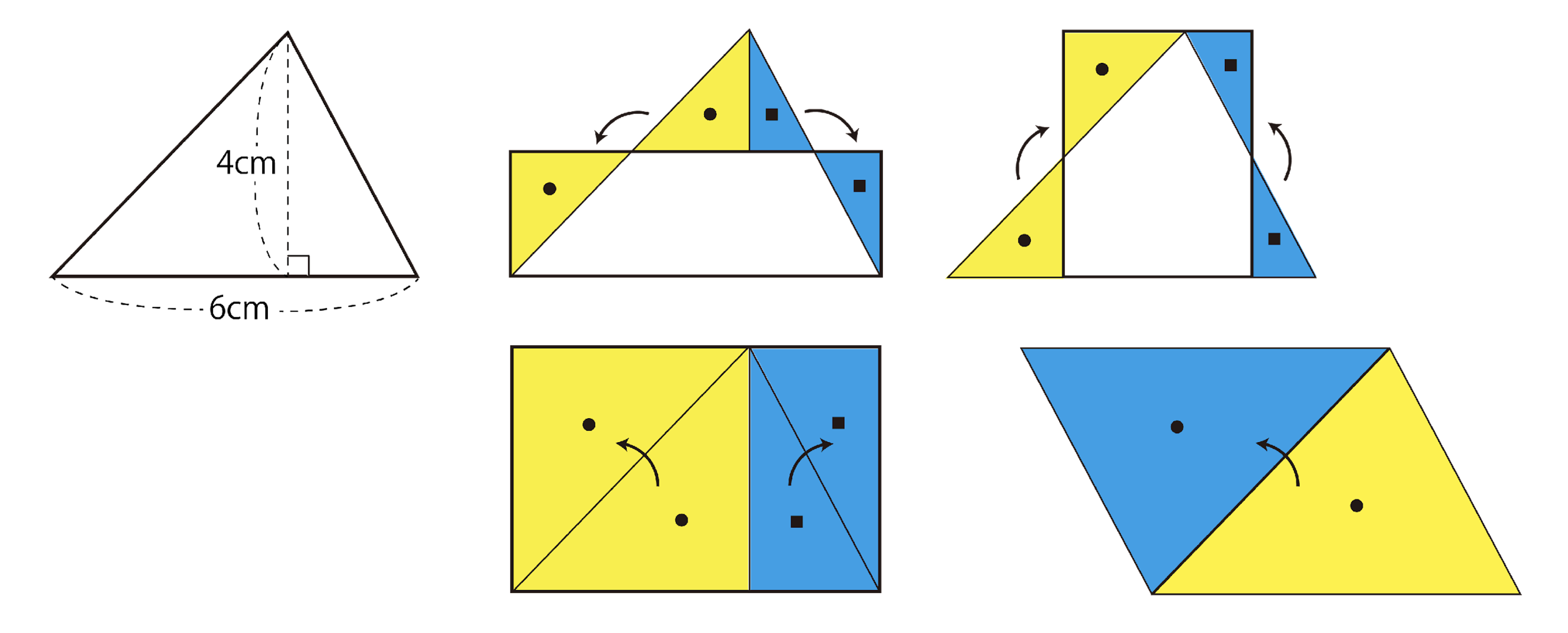
まず、第11時では、三角形の面積の求め方を様々な方法で改めて説明できるようになることを本時のめあてとしてグループワークを行います。第1~7時の中で行うミニレッスンの中でも、三角形の面積を求める考え方の1つを取り上げて説明しているものの、この時間で改めて三角形の面積を求め方に様々な考え方があることをグループで発見するように促します。
この段階では児童は三角形の面積を求める公式[底辺×高さ÷2]を覚えているため、計算方法でつまずくことがなく、面積を求める考え方の議論に集中できます。これにより多くの児童が一段と理解を深めることができます。
第12時では、少し特殊な形をした図形の面積を求める問題に皆で挑戦する時間にしています。一人一枚プリントを配ってペアやグループで協力しあって問題を解いていきます。
第11時で図形を分解することで変わった形の図形でも工夫をすれば面積を求められることに気づいているため、やや高いレベルの問題ではありますが、皆で協力しながら解いていきます。25分ほど経過したタイミングで考える時間を切り上げ、各々が考えた方法と答えを全体で共有する時間に切り替えます。最後にプリントを回収し、思考・表現・判断の評価に活用していきます。
さいごに
今回紹介したのは、小学生の図形の面積の範囲ですが、他の単元や中学生の数学でも同じように自由進度学習を取り入れて学習することは可能です。学びの手段が多様になり、個々にあったものを選びやすくなった今日では、このような学習者自身が主体的に学んでいく授業のあり方を益々デザインしやすくなりました。
今回紹介した授業はあくまで一例に過ぎませんが、授業づくりのヒントになれば幸いです。
